Welcome to Bellman Ford Method’s documentation!

Bellman Ford algorithm helps us find the shortest path from a vertex to all other vertices of a weighted graph.

The Bellman-Ford algorithm provides the shortest distance from a prespecified origin node to all other nodes in the graph (weighted digraph). It is able to handle graphs where some of the edge weights are negative numbers. The based idea is: show if there is a negative cycle, generate a negative cycle and always find a negative cycle (if there is one) even if the graph is not connected.

Bellman Ford’s Algorithm Applications

For calculating shortest paths in routing algorithms
For finding the shortest path

How Bellman Ford’s Algorithm Works

Bellman Ford algorithm works by overestimating the length of the path from the starting vertex to all other vertices. Then it iteratively relaxes those estimates by finding new paths that are shorter than the previously overestimated paths. By doing this repeatedly for all vertices, we can guarantee that the result is optimized.

Bellman Ford Pseudocode [reference]

We need to maintain the path distance of every vertex. We can store that in an array of size v, where v is the number of vertices.

We also want to be able to get the shortest path, not only know the length of the shortest path. For this, we map each vertex to the vertex that last updated its path length.

Once the algorithm is over, we can backtrack from the destination vertex to the source vertex to find the path.

function bf_negative_cycle(G)
  for each vertex V in G
    distance[V] <- infinite
      previous[V] <- NULL
  distance[S] <- 0

  for each vertex V in G
    for each edge (U,V) in G
      tempDistance <- distance[U] + edge_weight(U, V)
      if tempDistance < distance[V]
        distance[V] <- tempDistance
        previous[V] <- U

  for each edge (U,V) in G
    If distance[U] + edge_weight(U, V) < distance[V}
      Error: Negative Cycle Exists

  return distance[], previous[]

Function

bf_negative_cycle(graph)

Returns an iterator that represents the shortest distance cycle in the graph. The input parameter must be the negative logarithm of the distance matrix as a DiGraph object, for example, networkx.

graph

Negative logarithm of distances between nodes as a DiGraph object.

For example

   #Bellman Ford Algorithm
   from bellman_ford import bf_negative_cycle
   #Digraph object
   import networkx as nx

   #Negative log matrix as graph
   G = nx.DiGraph()
   G.add_weighted_edges_from(edges)

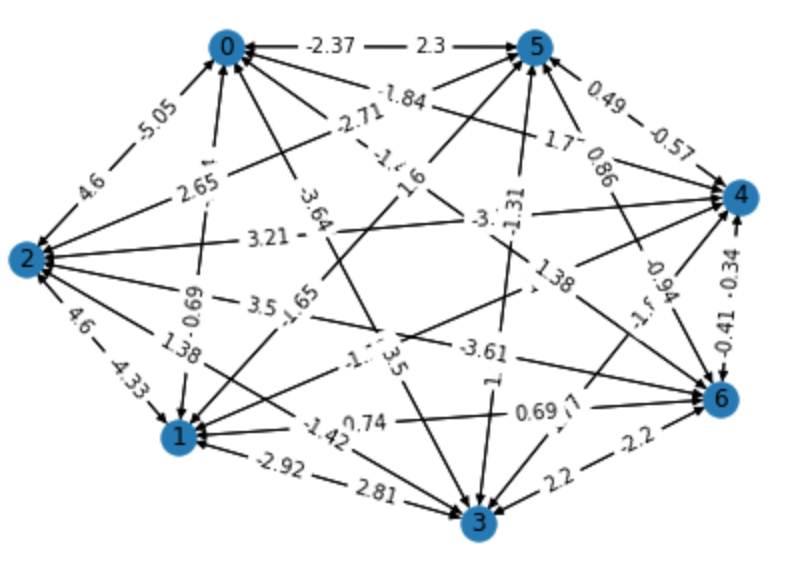
#Apply BF algorithm
bf_negative_cycle(G)

The output of the program is:

[5, 6, 5]

Installation

To install bellman_ford, simply run:

pip install git+https://github.com/optimizacion-2-2022-gh-classroom/practica-1-segunda-parte-pautrejo

If you encounter a bug or would like to participate in the further development of this package come find us on Github.